Hands-On: Mixed Integer Linear Programming for Last-Mile Delivery
Among others, pharmaceutical last-mile delivery involves medication delivery and medical equipment transport from a distribution center to pharmacies, clinics, medical centers, and more. Drug delivery systems must be highly reliable, efficient, and responsive to sudden changes in demand during emergencies and accidents.
What if the fastest way you could receive emergency care was through the sky?
Like the drone medical delivery of an AED that delivered the first shocks to a man who suffered cardiac arrest while scraping snow in Sweden - before ambulance personnel arrived1. Or drone-powered blood unit distribution in large cities and rural areas2. The point is that providing rapid access to life-saving equipment avoids harm in emergencies.
How does Mixed Integer Linear Programming help with distribution?
In essence, we want to solve a Capacitated Vehicle Routing Problem from the Operations Research field. Which is the optimization of the payload for each vehicle, ensuring that the most critical payloads are prioritized and determining the optimal routes for drones to minimize lead time. The goal is to maximize care by mixing two known Integer Programming problems:
- Load Capacity (Knapsack Problem)
- Time Urgency (Traveling Salesman Problem)
In combination, the algorithm selects payload and addresses delivery sequencing within a MILP Problem, a.k.a. the Capacitated Vehicle Routing Problem.
Ultimately, this tutorial helps logistics professionals, analysts and business consultants understand how to use Quantagonia’s Hybrid Solver to calculate these mathematical problems.
How to Implement Mixed Integer Linear Programming in Python
Setting up an Optimization Problem in Python is a straightforward process.
- Define Problem Parameters (e.g. Delivery locations)
- Define Objective Function (e.g. Minimize total distance)
- Define Constraint Functions (e.g. Vehicle capacity)
- Optimize Model
- Process the Results
This structure ensures clarity, making it easier to understand and modify the code later on.
Code Implementation: Optimizing Drone Deliveries for Munich
By way of example, we generate random locations within Munich. Each drone has an item-carry limit of three, with each location needing one. The goal is to administer all drone deliveries as fast as possible (minimize cost, which is distance in this case). If a drone has supplied its three items, it has to restock at the warehouse.
From there, we can formulate the constraints:
- meet the demands of every location
- do not exceed the capacity of a drone
- don’t allow double visits within a tour
- ensure the elimination of sub-tours
We then pass the Model to the HybridSolver API and solve for the most efficient routes.
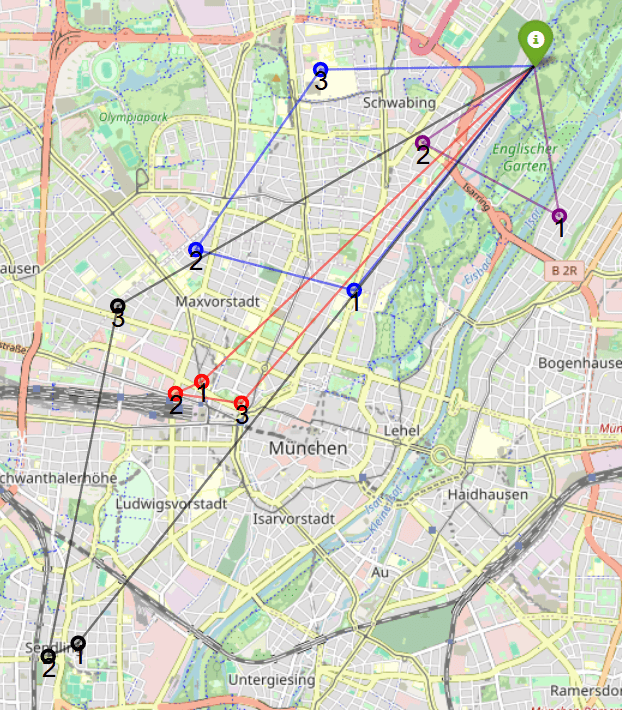
The solution groups similar locations into a single trip. However, the routing can become increasingly more complex once you introduce multiple drones, variable payloads, and different warehouses. Try it out yourself. Here is the code implementation of the Tutorial.








